sin2x与tanx的转化(sin2x和tanx的转化公式)
sin2x=2sinxcosx tanx=sinxcosx 即2sinxcosx=sinxcosx 化简得2cos^2x=1 cosx=正负2分之根号2 下面x即可求出,注意两解。
sinx=2cosx,sinx^2+12sinx^2=1,得sinx^2=45,sin2x=2sinxcosx=sinx^2=45希望采纳 谢谢。
这个是二倍角公式sin2x=2sinxcosx tan2x=2tanx1tanx^2cos2x=cosx^2sinx^2=2cosx^21=12sinx^2 倍角公式 倍角公式,是三角函数中非常实用的一类公式就是把二倍角的三角函数用本角的。
不好意思,刚才写错了一点点应该是y#39=sin2x#39+tanx#39=2x#39cos2x+1cosx^2=2cos2x+1cosx^2。
二倍角公式sin2x=2sinxcosxcos2x=cosx^2sinx^2=2cosx^21=12sinx^2tan2x=2tanx1tanx^2tan2x=sin2xcos2x, cot2x=cos2xsin2x因此原式=sin2x1sin2xcos2x+cos2x1cos2x。
方法如下,请作参考。
标签: sin2x与tanx的转化
相关文章
-
sin2x与tanx的转化(tanx与sin2x的转换关系)详细阅读
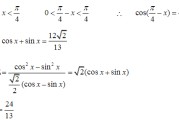
1、二倍角公式sin2x=2sinxcosxcos2x=cosx^2sinx^2=2cosx^21=12sinx^2tan2x=2tanx1tanx^...
2022-06-01 93 sin2x与tanx的转化

发表评论